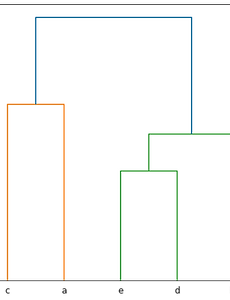
 계층적 군집화
계층적 군집(Hierarchical Clustering)은 n개의 군집으로 시작해 점차 군집의 개수를 줄여 나가는 방법입니다. 유클리디안 거리를 사용해서 계층적 군집분석을 시행해 보겠습니다. import matplotlib.pyplot as plt import numpy as np from scipy.cluster.hierarchy import dendrogram, linkage X = np.array([[1, 4], [2, 1], [4, 6], [4, 3], [5, 1]]) labels = ['a', 'b', 'c', 'd', 'e'] plt.figure(figsize=(7, 7)) plt.xlim(0, 7) plt.ylim(0, 7) plt.scatter(X[:, 0], X[:, 1]) for lab..
2022. 8. 15.
계층적 군집화
계층적 군집(Hierarchical Clustering)은 n개의 군집으로 시작해 점차 군집의 개수를 줄여 나가는 방법입니다. 유클리디안 거리를 사용해서 계층적 군집분석을 시행해 보겠습니다. import matplotlib.pyplot as plt import numpy as np from scipy.cluster.hierarchy import dendrogram, linkage X = np.array([[1, 4], [2, 1], [4, 6], [4, 3], [5, 1]]) labels = ['a', 'b', 'c', 'd', 'e'] plt.figure(figsize=(7, 7)) plt.xlim(0, 7) plt.ylim(0, 7) plt.scatter(X[:, 0], X[:, 1]) for lab..
2022. 8. 15.